[인공지능] 인공지능 기초 - Gradient Descent

인공지능은 스스로 Parameter를 조정하여 정답을 만들어낸다.

이 때, Parameter를 조정하기 위해서는 Optimize(최적화)를 해야 하는데,

Optimize에서 쓸 수 있는 방법들을 Optimizer라고 한다.

 

오늘은 Optimizer의 가장 기본 중의 기본인 Gradient Descent(경사하강법)에 대하여 알아볼 것이다.

 

1. Gradient Descent (경사하강법)

먼저 아래와 같은 이차 함수 그래프를 보자

이차함수와 -5에서의 접선

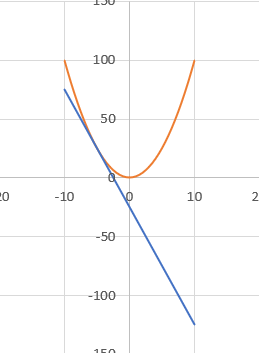
이 그래프에서 현재 x가 -5라고 가정하자. 우리는 y를 최소로 하고 싶다면 어떻게 해야 하겠는가?

그렇다. x를 0으로 바꾸면 된다. 그러나, 우리들이 이 함수가 이차함수 y = x^2임을 모르거나, 해석하기 어려울 정도로 복잡한 함수라면? 우리들이 알 수 있는 것은 접선의 기울기(혹은 미분값) 뿐이면 우리들은 아래와 같은 방식으로 이를 해결할 수 있다.

$$ x_t = x_t-1 - \mu \delta f(x) $$

 

이때, $\mu = step size$이다.

 

이 식을 위의 이차함수 그래프에 적용하면

현재 x=-5일 때, 기울기가 -10이고, $\mu$를 0.1이라고 가정하면

$$ x = -5 - (-10) \mu = -4 $$

이므로, y가 25에서 16으로 줄어들었음을 알 수 있다.

 

이렇게 점차 y를 줄여나가는 방식을 Gradient Descent라고 한다.

이를 이용하면 수식으로 표현하기 어려운 함수, 해석하기 어려운 함수, 다변수 함수 등의

최솟값을 찾기 어려운 함수의 최솟값을 찾을 수 있다.

 

2. step size($\mu$) 설정

step size는 hyperparameter로 프로그램이 실행되기 이전에 우리가 직접 설정해 주어야 하는 변인이다.

 

이 값은 매우 중요한데, 다시 한번 이차함수를 살펴보자

이차함수와 -5에서의 접선

$\mu$가 2일 때를 생각해보자. x = -5이다.

$$ x = -5 - (-10) \mu = 15 $$

x가 15가 되며 방향은 최솟값으로 향했지만 너무 많이 이동하여 y가 오히려 올라갔다.

$\mu$가 너무 크면 이러한 방식으로 점차 y가 올라가는 진동현상이 발생한다.

 

$\mu$가 0.001일 때는?

$$ x = -5 - (-10) \mu = -4.99 $$

$\mu$가 너무 작으면 한번 움직일 때 매우 작은 변화만이 생겨, 결과적으로 0에 가까워지기는 하나 수많은 연산을 필요로 할 것이다.

 

따라서, 여러 실험을 통해 $\mu$를 알맞은 값으로 조정해야 한다.

 

3. 결론

이번 포스팅에서는 Gradient Descent에 대하여 알아보았다. 이는 Parameter에 대한 Loss의 기울기를 알게 되면, Parameter를 Loss가 0으로 가까워지도록 조정할 수 있다는 것이다.

Deep Learning에서는 Gradient Descent를 비롯한 다양한 Optimizer를 이용해 Parameter를 알맞게 조절하여 학습하는 것이다.

 

Gradient Descent는 Deep Learning에서 중요한 개념 중 하나이므로 꼭 익혀두길 바란다.